PostgreSQl 최단경로 계산 방법에 대해 설명합니다. PostgreSQL을 사용하는 이유는 최단경로를 그리기 위한 다양한 알고리즘을 제공합니다. GIS 기능에 특화된 유용한 pgrouting 기능을 활용해 간단한 쿼리명령 하나로 최단경로를 구할 수 있습니다.
목차
Toggle목표
두 지점 간의 가장 짧은 이동 거리를 추정하여 계산합니다.
PostgreSQL 최단경로 생성 방법
- 이동 경로를 아래와 같이 설정합니다.
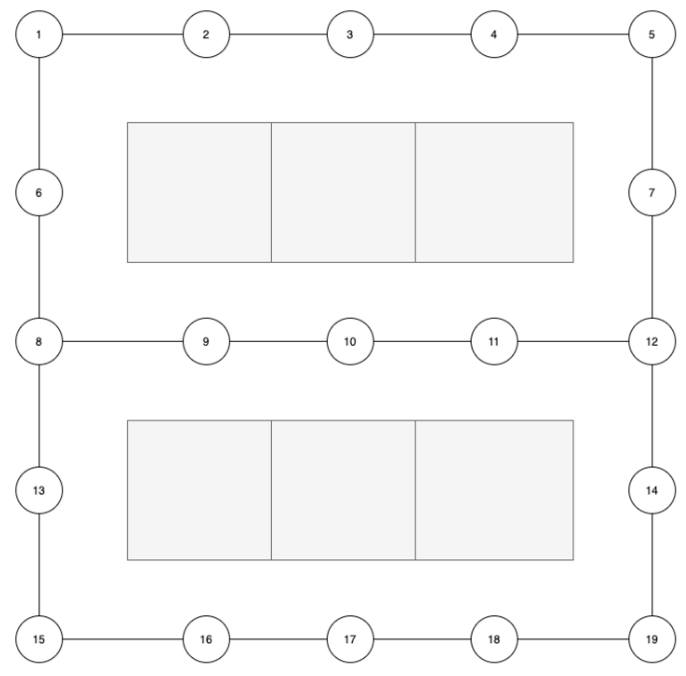
- 이동 경로 동선을 생성해 PostgreSQL DB에 저장합니다.
PostgreSQL 최단경로 테이블 설정 방법
- 해당 경로를 PostgreSQL DB에 저장합니다. 단, 최단경로를 구할 수 있는 데이타 형태로 DB가 추가 되어야 합니다.
Edges 테이블
| Column | Description | 비고 |
|---|---|---|
| id | 고유 ID | indexed |
| source | 시작점 ID | indexed |
| target | 도착점 ID | indexed |
| cost | source → target 비용 | 최단 거리 계산에 사용(실제 거리 입력) |
| reverse_case | target → source 비용 | 최단 거리 계산에 사용(실제 거리 입력) |
| capacity | source → target | 미사용이면 100로 설정 |
| reverse_capacity | target → source | 미사용이면 100로 설정 |
| x1 | starting point x | |
| y1 | starting point y | |
| x2 | end point x | |
| y2 | end point y | |
| geom | line geometry | indexed |
Edges Table 생성
CREATE TABLE edges (
id BIGSERIAL PRIMARY KEY,
source BIGINT,
target BIGINT,
cost FLOAT,
reverse_cost FLOAT,
capacity BIGINT,
reverse_capacity BIGINT,
x1 FLOAT,
y1 FLOAT,
x2 FLOAT,
y2 FLOAT,
geom geometry
);
Example
- Insert Data into Edges
INSERT INTO edges (
cost, reverse_cost,
capacity, reverse_capacity, geom) VALUES
( 1, 1, 80, 130, ST_MakeLine(ST_POINT(2, 0), ST_POINT(2, 1))),
(-1, 1, -1, 100, ST_MakeLine(ST_POINT(2, 1), ST_POINT(3, 1))),
(-1, 1, -1, 130, ST_MakeLine(ST_POINT(3, 1), ST_POINT(4, 1))),
( 1, 1, 100, 50, ST_MakeLine(ST_POINT(2, 1), ST_POINT(2, 2))),
( 1, -1, 130, -1, ST_MakeLine(ST_POINT(3, 1), ST_POINT(3, 2))),
( 1, 1, 50, 100, ST_MakeLine(ST_POINT(0, 2), ST_POINT(1, 2))),
( 1, 1, 50, 130, ST_MakeLine(ST_POINT(1, 2), ST_POINT(2, 2))),
( 1, 1, 100, 130, ST_MakeLine(ST_POINT(2, 2), ST_POINT(3, 2))),
( 1, 1, 130, 80, ST_MakeLine(ST_POINT(3, 2), ST_POINT(4, 2))),
( 1, 1, 130, 50, ST_MakeLine(ST_POINT(2, 2), ST_POINT(2, 3))),
( 1, -1, 130, -1, ST_MakeLine(ST_POINT(3, 2), ST_POINT(3, 3))),
( 1, -1, 100, -1, ST_MakeLine(ST_POINT(2, 3), ST_POINT(3, 3))),
( 1, -1, 100, -1, ST_MakeLine(ST_POINT(3, 3), ST_POINT(4, 3))),
( 1, 1, 80, 130, ST_MakeLine(ST_POINT(2, 3), ST_POINT(2, 4))),
( 1, 1, 80, 50, ST_MakeLine(ST_POINT(4, 2), ST_POINT(4, 3))),
( 1, 1, 80, 80, ST_MakeLine(ST_POINT(4, 1), ST_POINT(4, 2))),
( 1, 1, 130, 100, ST_MakeLine(ST_POINT(0.5, 3.5), ST_POINT(1.999999999999, 3.5))),
( 1, 1, 50, 130, ST_MakeLine(ST_POINT(3.5, 2.3), ST_POINT(3.5, 4)));
( 1, 1, 80, 130, ST_MakeLine(ST_POINT(2, 0), ST_POINT(2, 1)))- 위 정보는 차례대로 이동거리(cost), 반대방향 이동거리(reverse_cost), 가능 용적(capacity), 반대방향 가능 용적(reverse_capacity), edges 라인 geom정보(시작점 → 끝점)을 입력합니다.
- capacity 100, reverse_cost 100 로 설정합니다.
- 경로들의 시작점 P1(2,0), 끝점 P2(2,1), 그 사이의 거리 D(=4)를 백엔드에서 받으면 아래와 같이 테이블에 데이타를 넣습니다.
INSERT INTO edges (
cost, reverse_cost,
capacity, reverse_capacity, geom) VALUES
( 4, 4, 100, 100, ST_MakeLine(ST_POINT(2, 0), ST_POINT(2, 1))),
....Create Vertices Table
- 아래 쿼리를 실행하면 버텍스 테이블이 생성됩니다.
SELECT * INTO vertices
FROM pgr_extractVertices('SELECT id, geom FROM edges ORDER BY id');Update Source, target, x1, y1, x2, y2
- edges 테이블에 source, target, 시작점(x1, y1), 끝점(x2, y2)을 설정합니다.
/* -- set the source information */
UPDATE edges AS e
SET source = v.id, x1 = x, y1 = y
FROM vertices AS v
WHERE ST_StartPoint(e.geom) = v.geom;
/* -- set the target information */
UPDATE edges AS e
SET target = v.id, x2 = x, y2 = y
FROM vertices AS v
WHERE ST_EndPoint(e.geom) = v.geom;
위 과정을 거치면 최단 경로를 구하는 Edges 테이블은 완성되었습니다.
- Undirect path(방향성이 없는 경로)
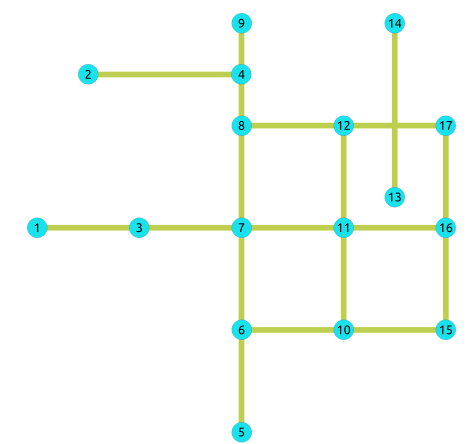
- Direct path(방향성이 있는 경로)
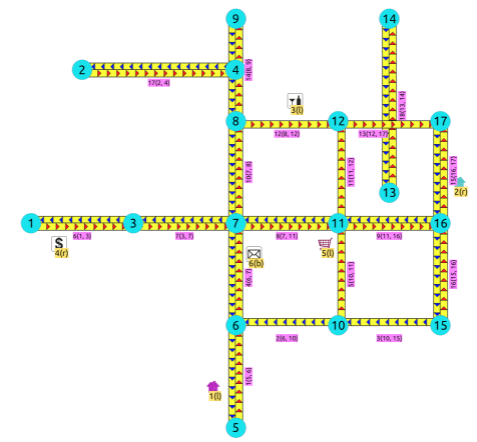
PostgreSQL 최단경로 계산
1956년에 개발된 Dijkstar 알고리즘을 사용합니다. 그래프 서칭 알고리즘 형태로 각 경로의 Cost를 계산해 Cost가 최소인 최단경로를 찾는 방식입니다.
Cost가 양의 값인 경우에 서칭 알고리즘이 작동되고 음수값이면 엣지가 존재하지 않는 걸로 인식됩니다.
시작과 목적지가 같으면 0을 반환하고 시작점과 목적지에 경로가 없으면 무한대값이 나옵니다.
아래 명령어를 입력하면 최적의 패스가 나옵니다.
- 방법
pgr_dijkstra(Edges SQL, start vid, end vid, [directed])
pgr_dijkstra(Edges SQL, start vid, end vids, [directed])
pgr_dijkstra(Edges SQL, start vids, end vid, [directed])
pgr_dijkstra(Edges SQL, start vids, end vids, [directed])
pgr_dijkstra(Edges SQL, Combinations SQL, [directed])
RETURNS SET OF (seq, path_seq, start_vid, end_vid, node, edge, cost, agg_cost)
OR EMPTY SET
- Get Undirect Path → 방향성이 없는 경우
- 최단 이동 거리는 아래 방식을 사용합니다.
SELECT * FROM pgr_Dijkstra(
'select id, source, target, cost, reverse_cost from edges',
6, 10, false);
seq | path_seq | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 2 | 1 | 0
2 | 2 | 10 | -1 | 0 | 1
- Get Direct Path → 방향성이 있는 경우
SELECT * FROM pgr_Dijkstra(
'select id, source, target, cost, reverse_cost from edges',
6, 10, true);
seq | path_seq | start_vid | end_vid | node | edge | cost | agg_cost
-----+----------+-----------+---------+------+------+------+----------
1 | 1 | 6 | 10 | 6 | 4 | 1 | 0
2 | 2 | 6 | 10 | 7 | 8 | 1 | 1
3 | 3 | 6 | 10 | 11 | 9 | 1 | 2
4 | 4 | 6 | 10 | 16 | 16 | 1 | 3
5 | 5 | 6 | 10 | 15 | 3 | 1 | 4
6 | 6 | 6 | 10 | 10 | -1 | 0 | 5
(6 rows)
- cost 를 다 더하면 6->10 으로 지게차가 이동한 거리가 됩니다. 위 예에서 cost를 1로 설정했기 때문에 방향성이 없는 경로에서는 1이 이동 거리가 됩니다. 방향성이 있는 경우는 6->7->11->16->15->10 으로 최단 경로가 나오고 총 이동 거리는 5가 됩니다.
참고사이트
- 경로 데이타 테이블 형식은 아래 사이트 참고
Sample Data — pgRouting Manual (3.5)
- 최적 경로 계산 방식 아래 사이트 참고